Math Open Ref constructions: A Comprehensive Guide
This article explores various geometric constructions found on Math Open Reference (mathopenref.com), a valuable resource for learning and understanding geometry. We’ll delve into the step-by-step processes for each construction, providing clear explanations and visualizable instructions. These constructions are fundamental to geometric understanding and have applications in various fields, from architecture to computer graphics.
Basic Constructions
# 1. Copying a Line Segment
This fundamental construction allows you to transfer the length of a line segment to another location.

1. Start with the given line segment AB. You want to copy this segment to a new location, starting at a point C.
2. Draw a ray starting at point C. This ray will define the direction of the copied segment.
3. Set your compass to the length of AB. Place the compass point on A and adjust the radius to reach B.
4. Without changing the compass setting, place the compass point on C and draw an arc that intersects the ray. The point of intersection, D, marks the end of the copied segment.
5. The line segment CD is now a copy of AB.
# 2. Bisecting a Line Segment
Bisecting a line segment means dividing it into two equal parts.
1. Start with line segment AB.
2. Set your compass to a radius greater than half the length of AB. This is crucial for the arcs to intersect.
3. Place the compass point on A and draw an arc that extends above and below the line segment.
4. Without changing the compass setting, place the compass point on B and draw an arc that intersects the first arc at two points. Label these points C and D.
5. Draw a line through points C and D. This line intersects AB at point E.
6. Point E is the midpoint of AB, and AE = EB.
# 3. Constructing a Perpendicular Bisector
The perpendicular bisector of a line segment is a line that is perpendicular to the segment and passes through its midpoint. This construction is essentially the same as bisecting a line segment.
1. Start with line segment AB.
2. Set your compass to a radius greater than half the length of AB.
3. Place the compass point on A and draw an arc that extends above and below the line segment.
4. Without changing the compass setting, place the compass point on B and draw an arc that intersects the first arc at two points. Label these points C and D.
5. Draw a line through points C and D. This line is the perpendicular bisector of AB. It intersects AB at point E.
6. Line CD is perpendicular to AB and AE = EB.
# 4. Constructing a Perpendicular Line at a Point on a Line
This construction creates a line perpendicular to a given line at a specific point on that line.
1. Start with line L and point P on L.
2. Place the compass point on P and draw two arcs that intersect line L on either side of P. Label these points A and B.
3. Set your compass to a radius greater than the distance from P to A (or B).
4. Place the compass point on A and draw an arc.
5. Without changing the compass setting, place the compass point on B and draw an arc that intersects the previous arc. Label the intersection point C.
6. Draw a line through points P and C. This line is perpendicular to L at point P.
# 5. Constructing a Perpendicular Line from a Point to a Line
This construction creates a line perpendicular to a given line that passes through a specific point not on the line.
1. Start with line L and point P not on L.
2. Place the compass point on P and draw an arc that intersects line L at two points. Label these points A and B.
3. Set your compass to a radius greater than half the distance between A and B.
4. Place the compass point on A and draw an arc below line L.
5. Without changing the compass setting, place the compass point on B and draw an arc that intersects the previous arc. Label the intersection point C.
6. Draw a line through points P and C. This line is perpendicular to L and passes through P.
Angle Constructions
# 6. Copying an Angle
This construction transfers the measure of an angle to a new location.
1. Start with angle BAC and ray DE. You want to copy angle BAC to ray DE.
2. Place the compass point on A and draw an arc that intersects both AB and AC. Label these points F and G, respectively.
3. Without changing the compass setting, place the compass point on D and draw an arc that intersects DE. Label the intersection point H.
4. Set your compass to the distance between F and G.
5. Without changing the compass setting, place the compass point on H and draw an arc that intersects the previous arc. Label the intersection point I.
6. Draw a line through D and I. Angle EDI is a copy of angle BAC.
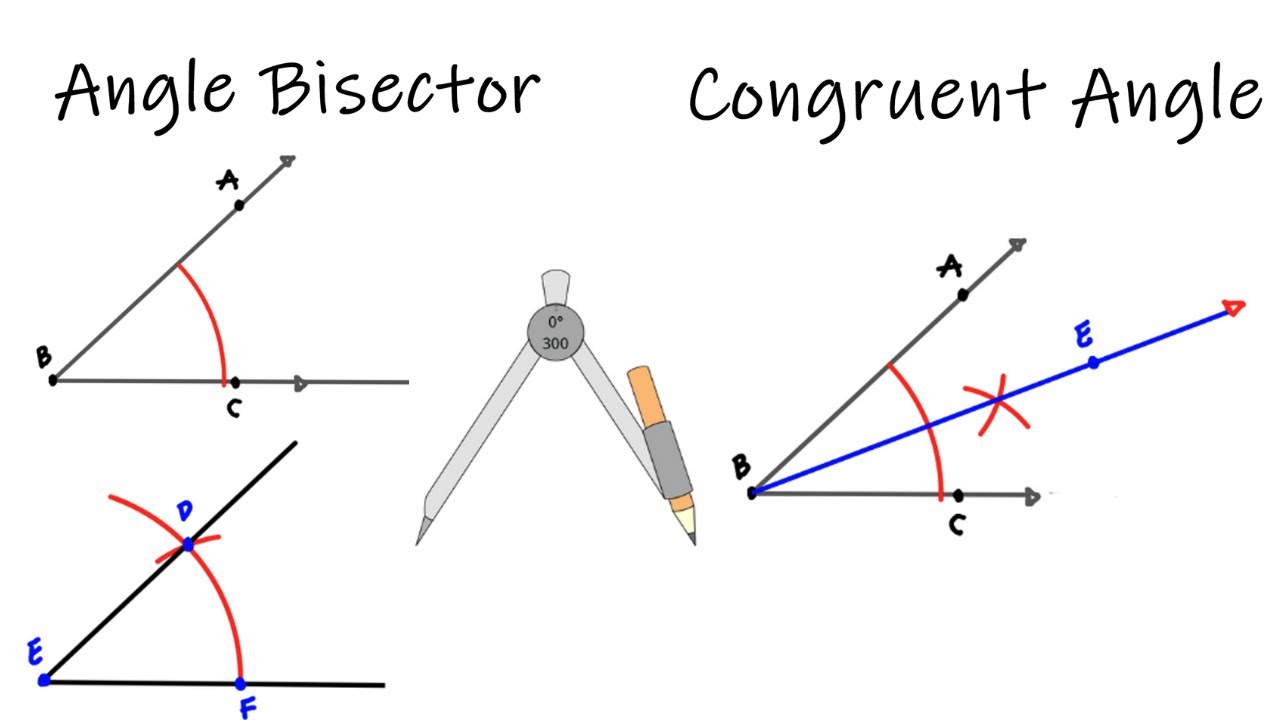
# 7. Bisecting an Angle
Bisecting an angle means dividing it into two equal angles.
1. Start with angle BAC.
2. Place the compass point on A and draw an arc that intersects both AB and AC. Label these points D and E, respectively.
3. Set your compass to a radius greater than half the distance between D and E.
4. Place the compass point on D and draw an arc.
5. Without changing the compass setting, place the compass point on E and draw an arc that intersects the previous arc. Label the intersection point F.
6. Draw a line through A and F. Line AF bisects angle BAC.
# 8. Constructing a 60-degree Angle
This construction creates an angle with a measure of 60 degrees.
1. Start with a ray AB.
2. Place the compass point on A and draw an arc that intersects AB. Label the intersection point C.
3. Without changing the compass setting, place the compass point on C and draw an arc that intersects the first arc. Label the intersection point D.
4. Draw a line through A and D. Angle DAB is a 60-degree angle.
# 9. Constructing a 30-degree Angle
This construction utilizes the bisection of a 60-degree angle to create a 30-degree angle.
1. Construct a 60-degree angle (as descriBed above). Let’s say you have angle DAB (60 degrees).
2. Bisect angle DAB (as described above). The bisecting line will create a 30-degree angle.
Triangle Constructions
# 10. Constructing a Triangle Given Three Sides (SSS)
This construction creates a triangle when the lengths of all three sides are known.
1. Start with three line segments representing the side lengths (a, b, and c).
2. Draw a line segment equal to one of the sides (e.g., side a). Label the endpoints A and B.
3. Set your compass to the length of side b. Place the compass point on A and draw an arc.
4. Set your compass to the length of side c. Place the compass point on B and draw an arc that intersects the previous arc. Label the intersection point C.
5. Draw line segments AC and BC. Triangle ABC is the desired triangle.
# 11. Constructing a Triangle Given Two Sides and the Included Angle (SAS)
This construction creates a triangle when the lengths of two sides and the angle between them are known.
1. Start with two line segments (a and b) and an angle (∠C).
2. Draw a line segment equal to one of the sides (e.g., side a). Label the endpoints A and B.
3. Construct angle ∠C at point A.
4. On the ray forming the other side of ∠C, mark a point D such that AD is equal to the length of side b.
5. Draw line segment BD. Triangle ABD is the desired triangle.
# 12. Constructing a Triangle Given Two Angles and the Included Side (ASA)
This construction creates a triangle when the measures of two angles and the length of the side between them are known.
1. Start with two angles (∠A and ∠B) and a line segment (side c).
2. Draw a line segment equal to side c. Label the endpoints A and B.
3. Construct angle ∠A at point A.
4. Construct angle ∠B at point B.
5. The point where the rays forming the other sides of the angles intersect is the third vertex, C. Triangle ABC is the desired triangle.
These constructions represent a foundational set of geometric tools. Mastering them is essential for further exploration in geometry and related fields. Math Open Reference provides excellent interactive demonstrations of these constructions, making
math open ref constructions
